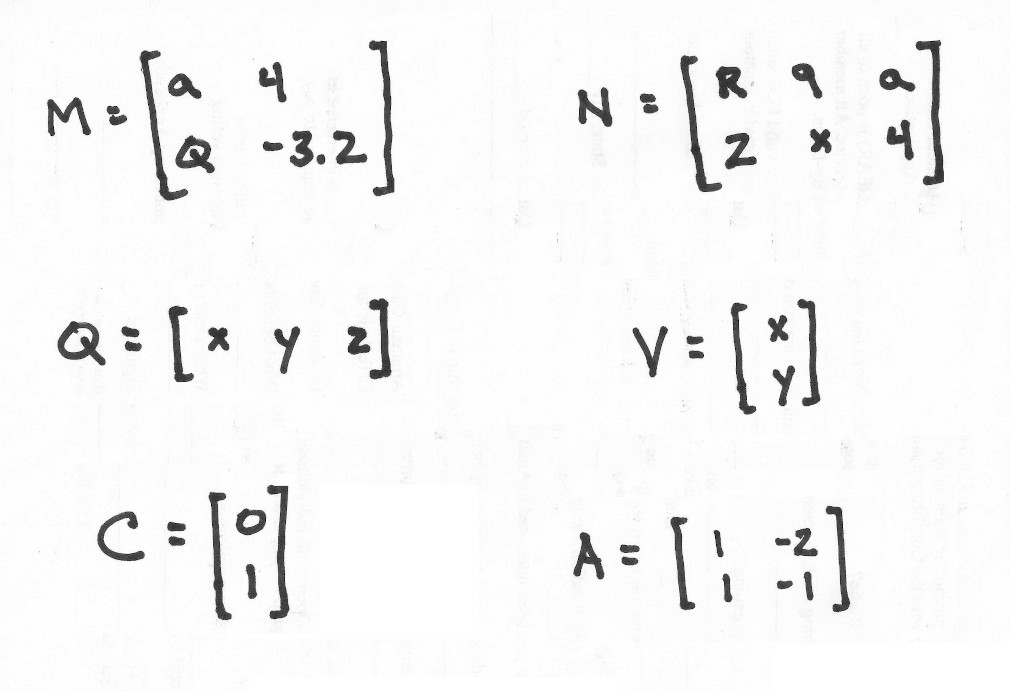Matrices

[last updated: 2024-03-08]

Matrix Determinants
Matrices to Solve Linear Equations
Vectors
-----

• A Matrix (pl. Matrices):
  is a rectangular grid or array of numbers or symbols, in rows and columns.
  

  M, N, Q, V, C, and A are examples of different matrices.

  • Matrices have some number of rows and columns of numbers or symbols.
    In the image above, matrices M and A have 2 rows and 2 columns.
    Matrix N has 2 rows and 3 colums,
    matrices V and C have 2 rows and 1 column,
    and matrix Q has 1 row and 3 columns.

  • The numbers or symbols in a matrix are elements, and can represent numbers, or coefficients of variables in a mathematical expression, or they can even represent whole matrices.

  • The Dimension of a matrix gives the number of rows and columns in the matrix, represented as m x n (row x column)
    In the image above, matrices M and A have dimension "2 x 2".
    The dimension of V and C is "2 x 1",
    the dimension of N is "2 x 3",
    and the dimension of Q is "1 x 3".

  • Special Matrices:
    • Square matrix: m = n
      • A Determinant can be calculated from a square matrix.
        The determinant is a scalar, and is used to calculate an Inverse Matrix (if one exists).
        It is also used in solving a system of linear equations, ...
      • A square matrix May have an Inverse Matrix.

    • If A is a non-square m x n matrix, you have two cases:
      • 1) If m is less than n, then the inverse image of y\in R^m usually exists but it is not unique. Therefore, the inverse mapping of x \mapsto Ax does not exist (except as a set function).
      • 2) If m is greater than n, then the image set of R^n in the mapping x \mapsto Ax is a proper subspace of R^m, and if you pick a point from the orthogonal complement of this subspace, you can't find the inverse image.
        • To better understand the idea, see the Rank-nullity theorem:
          https://en.wikipedia.org/wiki/Rank%E2%80%93nullity_theorem
        • However, you can find the so-called pseudoinverse
          https://en.wikipedia.org/wiki/Pseudoinverse
          for any matrix by using the singular value decompostion (svd).
          https://en.wikipedia.org/wiki/Singular_value_decomposition
          It is not the actual inverse matrix, but the "best approximation" of such in the sense of least squares
          https://en.wikipedia.org/wiki/Least_squares
        • However, if the actual inverse matrix exists, the pseudoinverse coincides with it. For example, in MATLAB you can find the pseudoinverse A by using the command pinv(A).

    • Column matrix: n = 1, ie. dimension is m x 1
      Used to represent vectors

    • Row matrix: m = 1, ie. dimension is 1 x n

    • Identity matrix

    • Null matrix

• Matrices can be used to solve a set/system of linear equations:

• Matrices can be used to do graphical manipulations:
  • Graphical plots/images are composed of points on a plane or in space.
    Each point is defined and represeneted as a vector, which is a line beginning at the origin and ending at the point being defined.
    Vectors therefore are directional, and represented as arrows, with their base at the origin and the arrow tip at the point being defined.
  • Basic manipulations are: Translation, Scaling, and Rotation..

• Operations on and between matrices:
  • Addition and Subtraction of two matrices - only between matrices of equal dimensions
  • Scalar multiplication - multiply a matrix by a number (scalar)
  • Matrix Multiplication of two matrices - the number of rows in the first matrix must be equal to the number of columns in the second matrix
    Note: Matrix multiplication is not commutative. That is, A x B ≠ B x A
  • Inverse matrix - used to effectively "divide" matrices
  • Transpose a matrix - takes each row of a matrix and converts it to a column
  • Cross product of two matrices - used for vectors
    A vector is a line with direction. Two lines define a plane.
    The cross-product of two vectors results in a vector perpendicular to the plane created by the two starting vectors.
    (can only be done with 3-dimensional vectors ?)
  • Dot product of two matrices - used for vectors
    The dot product results in a scalar that is the angle between the two vectors
  • Normalization:
    Given a vector of some length and angle, the process of Normalization creates a vector of length 1 (a Unit Vector) in the same direction.

  • Elementary Row Operations:
    These are operations performed on a matrix that preserve its equality:
    • Row switching (swap): Swap two rows of a matrix.
    • Row multiplication (scale): Multiply a row of a matrix by a nonzero constant.
    • Row addition (pivot): Add to one row of a matrix some multiple of another row.

  
  -----

• Links:
  • also search for: determinants, eigenvectors, eigenvalues, vectors, tensors, Cramer's rule, gaussian elimination,
  • https://news.mit.edu/2013/expl ained-matrices-1206
  • webGL:
    https://www.tutorialspoint.com/webgl/index.htm
    https://www.khronos.org/webgl/wiki/Main_Page
    http://learnwebgl.brown37.net/index.html
    https://webglsamples.org/
    https://developer.mozilla.org/en-US/docs/Web/API/WebGL_API/By_example
    http://learnwebgl.brown37.net/transformations2/transformations_matrices....
  • https://www.haroldserrano.com/blog/matrices-in-computer-graphics
  • https://www.haroldserrano.com/blog/vectors-in-computer-graphics
  • https://courses.lumenlearning.com/boundless-algebra/chapter/using-matric...
  • https://en.wikipedia.org/wiki/Matrix_(mathematics)
  • https://iq.opengenus.org/3d-array-in-c/
  • basis vector: https://en.wikipedia.org/wiki/Basis_(linear_algebra)
  • rotation matrix: https://en.wikipedia.org/wiki/Rotation_matrix
  • ancient chinese rod calculus: https://en.wikipedia.org/wiki/Rod_calculus#System_of_linear_equations
  • linear algebra: https://en.wikipedia.org/wiki/Linear_algebra
  • https://en.wikipedia.org/wiki/Graphics_pipeline
  • https://en.wikipedia.org/wiki/Transformation_matrix
  • https://en.wikipedia.org/wiki/3D_projection
  • search for: 3d graphics with matrices
  • vector cross product: https://www.cuemath.com/geometry/cross-product/
    https://byjus.com/maths/cross-product/
    https://en.wikipedia.org/wiki/Cross_product
    in dimension > 3: https://www.youtube.com/watch?v=lZbz_icXkJc
  • search/study: quaternions, octonions, wedge product
  • normed division algebra:
    https://www.scientificlib.com/en/Mathematics/Algebra/NormedDvisionAlgebr...
    https://ncatlab.org/nlab/show/normed+division+algebra
    https://en.wikipedia.org/wiki/Hurwitz%27s_theorem_(composition_algebras)
  • https://www.w3.org/TR/REC-MathML/chap3_5.html
  • https://www.tutorialspoint.com/mathml/mathml_matrices.htm
  • https://en.wikipedia.org/wiki/Matrix_multiplication
  • https://en.wikipedia.org/wiki/Pseudo-determinant
  • https://mathinsight.org/determinant_geometric_properties

.

.

.

eof