Calculate distance between two GPS coordinates

[last updated: 2022-03-06]
GPS module
tracker software
calculation resource material
-----

from:
https://en.wikipedia.org/wiki/Great-circle_distance
• distance(miles) = radius(miles) * centralAngle(radians)

• centralAngle using standard spherical trig:
  • Given two GPS coordinates: lat1, lng1, and lat2, lng2
  • centralAngle = arccos ( [ sin(lat1) * sin(lat2) ] + [ cos(lat1) * cos(lat2) * cos( | lng2 - lng1 | ) ]

  • This formula can be fairly accurate for small distances
    if calculations are done using 64-bit floating point processors.
    However the haversine method below can be more accurate

  • However:
    Calculating a distance of ~ 1/2 mile using both methods
    resulted in a difference of only a few inches,
    much less than the error window in GPS coordinates (which is a few meters).
    My conclusion: Use the Central Angle formula above from standard spherical trig,
    and avoid the complexity of the haversine equations.

• centralAngle using haversines:
  • If you have a processor with limited precision, you may still want to use this haversine formula:
    
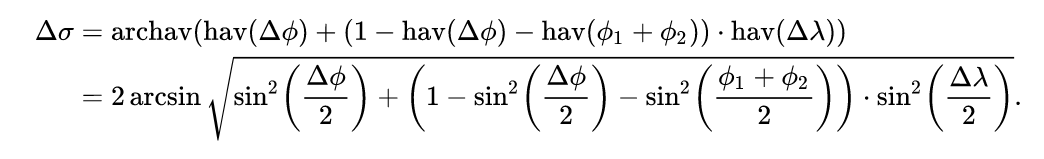
  • where: phi = latitude, lambda = longitude

• Haversines:
  • from: https://en.wikipedia.org/wiki/Haversine_formula

.

.

.

eof